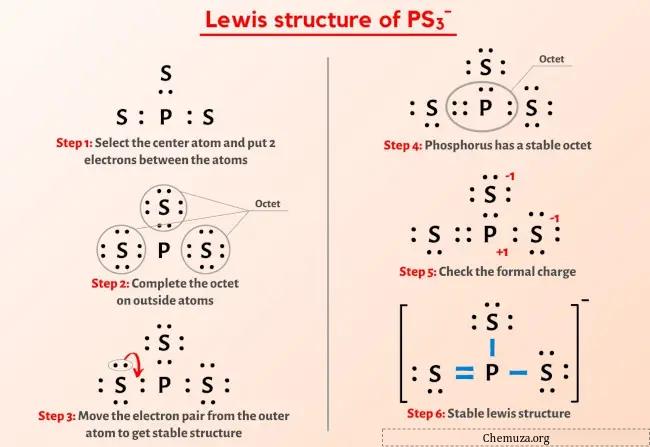
上の画像はもう見たはずですよね?
上の画像について簡単に説明します。
PS3-Lewis 構造の中心にはリン (P) 原子があり、その周りを 3 つの硫黄 (S) 原子が取り囲んでいます。リン (P) 原子と各硫黄 (S) 原子の間には 1 つの二重結合と 2 つの単結合があります。二重結合硫黄原子 (S) には 2 つの非共有電子対があり、単結合硫黄原子 (S) には 3 つの非共有電子対があります。
上の PS3-Lewis 構造の図を見て何も理解できなかった場合は、PS3-Lewis 構造の描画に関する詳細なステップバイステップの説明が表示されますので、そのままお付き合いください。
それでは、PS3 のルイス構造を描く手順に進みましょう。
PS3-ルイス構造描画手順
ステップ 1: PS3 イオンの価電子の総数を求める
PS3 イオンの価電子の総数を知るには、まずリン原子と硫黄原子に存在する価電子を知る必要があります。
(価電子は、原子の最も外側の軌道に存在する電子です。)
ここでは、周期表を使ってリンと硫黄の価電子を簡単に求める方法を説明します。
PS3 イオンの総価電子
→ リン原子によって与えられる価電子:
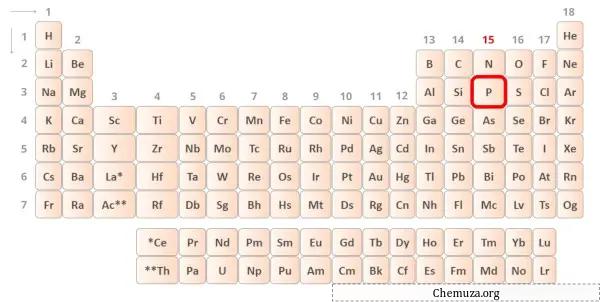
リンは周期表の第 15 族の元素です。 [1]したがって、リンに存在する価電子は5です。

上の画像に示すように、リン原子には 5 つの価電子が存在することがわかります。
→ 硫黄原子によって与えられる価電子:
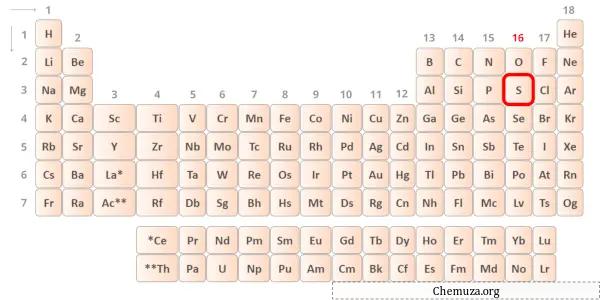
硫黄は、周期表の第 16 族の元素です。 [2]したがって、硫黄に存在する価電子は6です。
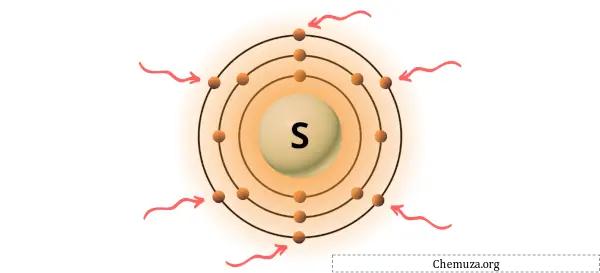
上の画像に示すように、硫黄原子には 6 つの価電子が存在することがわかります。
それで、
PS3 イオンの総価電子= 1 つのリン原子によって供与された価電子 + 3 つの硫黄原子によって供与された価電子 + 1 つの負電荷により 1 つの余分な電子が追加 = 5 + 6(3) + 1 = 24 。
ステップ 2: 中心原子を選択する
中心原子を選択するには、最も電気陰性度の低い原子が中心に残ることを覚えておく必要があります。
ここで、与えられたイオンは PS3- イオンであり、これにはリン (P) 原子と硫黄 (S) 原子が含まれています。
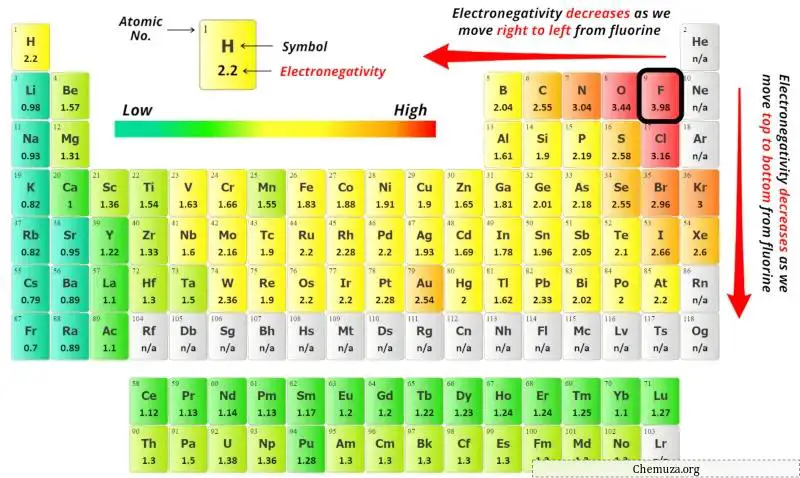
上の周期表のリン(P)原子と硫黄(S)原子の電気陰性度の値を確認できます。
リン (P) と硫黄 (S) の電気陰性度の値を比較すると、リン原子の方が電気陰性度が低くなります。
ここで、リン (P) 原子が中心原子、硫黄 (S) 原子が外側の原子です。

ステップ 3: 各原子の間に電子対を配置して各原子を接続する
PS3 分子では、リン原子 (P) と硫黄原子 (S) の間に電子対を配置する必要があります。
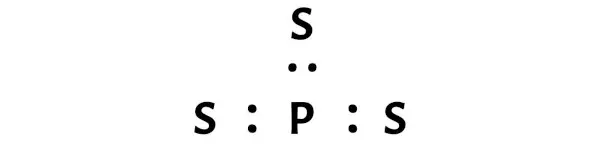
これは、PS3分子内でリン(P)と硫黄(S)が化学結合していることを示しています。
ステップ 4: 外部原子を安定化する
このステップでは、外部原子の安定性をチェックする必要があります。
ここの PS3 分子のスケッチでは、外側の原子が硫黄原子であることがわかります。
これらの外部硫黄原子はオクテットを形成するため、安定しています。
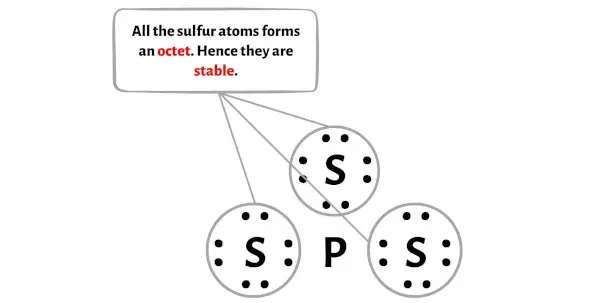
さらに、ステップ 1 では、PS3 イオンに存在する価電子の総数を計算しました。
PS3 イオンには合計24 個の価電子があり、これらすべての価電子が上の図で使用されています。
したがって、中心原子上に保持すべき電子の対はもう存在しません。
それでは、次のステップに進みましょう。
ステップ 5: 中心原子のオクテットを確認します。オクテットがない場合は、非共有電子対を移動して二重結合または三重結合を形成します。
このステップでは、中心のリン (P) 原子が安定であるかどうかを確認する必要があります。
中心のリン (P) 原子の安定性を確認するには、それがオクテットを形成しているかどうかを確認する必要があります。
残念ながら、ここではリン原子はオクテットを形成しません。リンは電子が6個しかなく、不安定です。
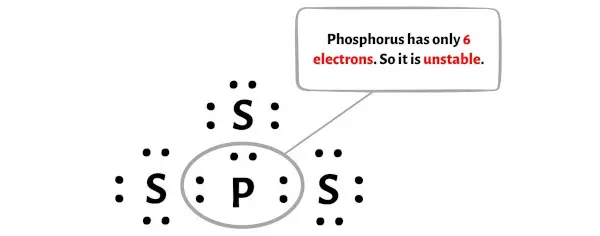
ここで、このリン原子を安定させるには、リン原子が 8 個の電子 (つまり 1 オクテット) を持つことができるように、外側の硫黄原子の電子対を移動する必要があります。
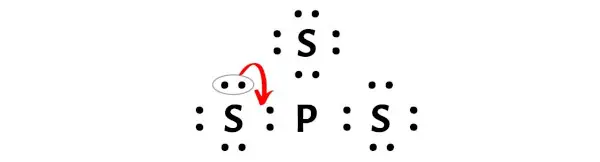
この一対の電子を移動させた後、中心のリン原子はさらに 2 つの電子を獲得し、その合計電子数は 8 になります。
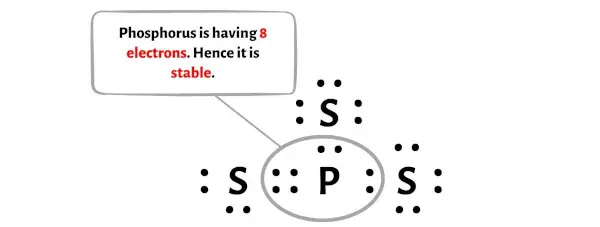
上の画像では、リン原子には 8 個の電子があるため、オクテットを形成していることがわかります。
それでは、上記のルイス構造が安定であるかどうかを確認する最後のステップに進みましょう。
ステップ 6: ルイス構造の安定性を確認する
これで、PS3 のルイス構造の安定性を確認する必要がある最後のステップに到達しました。
ルイス構造の安定性は、形式電荷概念を使用して検証できます。
つまり、PS3 分子に存在するリン (P) 原子と硫黄 (S) 原子の形式電荷を見つけなければなりません。
正式な税金を計算するには、次の式を使用する必要があります。
形式電荷 = 価電子 – (結合電子)/2 – 非結合電子
以下の画像で、各 PS3 イオン原子の結合電子と非結合電子の数を確認できます。
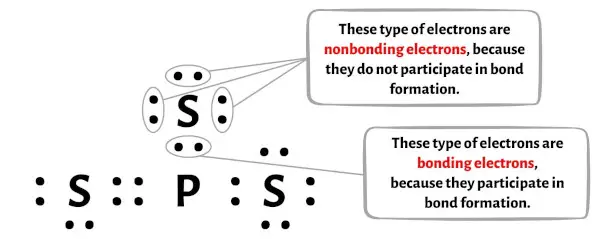
リン原子 (P) の場合:
価電子 = 5 (リンは 15 族にあるため)
結合電子 = 8
非結合電子 = 0
二重結合硫黄 (S) 原子の場合:
価電子 = 6 (硫黄は 16 族にあるため)
結合電子 = 4
非結合電子 = 4
単結合硫黄 (S) 原子の場合:
価電子 = 6 (硫黄は 16 族にあるため)
結合電子 = 2
非結合電子 = 6
| 正式な告発 | = | 価電子 | – | (結合電子)/2 | – | 非結合電子 | ||
| P. | = | 5 | – | 8/2 | – | 0 | = | +1 |
| S(ダブルホップ) | = | 6 | – | 4/2 | – | 4 | = | 0 |
| S(単結合) | = | 6 | – | 2/2 | – | 6 | = | -1 |
| S(単結合) | = | 6 | – | 2/2 | – | 6 | = | -1 |
上記の形式的な電荷計算から、リン (P) 原子の電荷は+1であるのに対し、単結合硫黄原子の電荷は-1であることがわかります。
それでは、これらの電荷を PS3 分子のそれぞれの原子に保持しましょう。
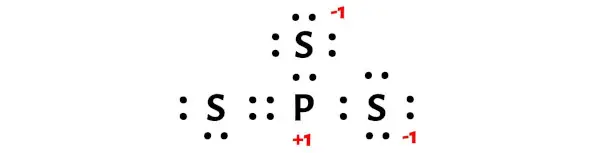
上のスケッチの+1と-1 の電荷はキャンセルされ、 -1 の電荷のみが上のスケッチに残り、PS3 分子には-1 の正式な電荷が生じます。
PS3 分子上のこの全体的な-1 の電荷は、下の図に示されています。
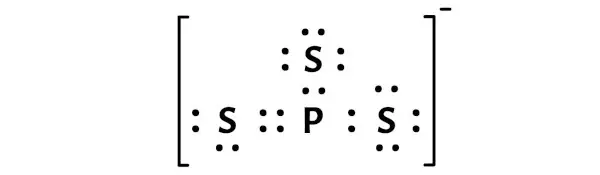
上記の PS3 イオンのルイス ドット構造では、結合電子の各ペア (:) を単結合 (|) として表すこともできます。そうすると、PS3-ion は次のようなルイス構造になります。
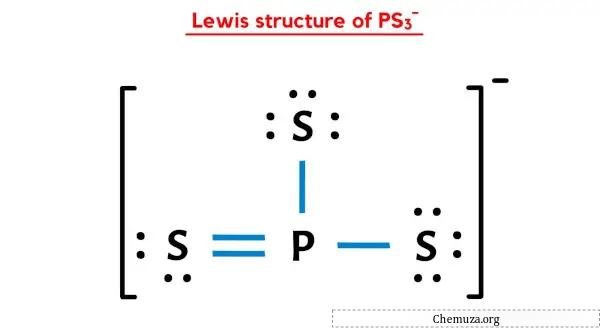
上記の手順をすべて完全に理解していただければ幸いです。
さらに練習して理解を深めたい場合は、以下にリストされている他のルイス構造を試してみてください。
理解を深めるために、次のルイス構造を試してください (または少なくとも見てください)。
