所以你已经看过上面的图片了,对吧?
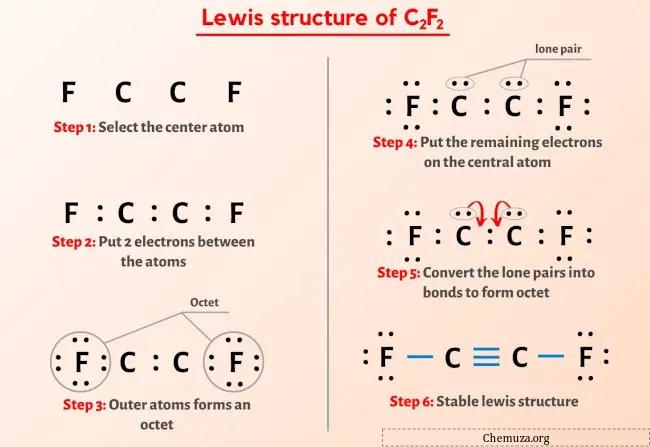
让我简单解释一下上图。
C2F2路易斯结构在两个碳(C)原子之间具有三键,在碳(C)原子和氟(F)原子之间具有单键。两个氟(F)原子上有3个孤对电子。
如果您对上图的 C2F2 路易斯结构没有理解任何内容,那么请继续关注我,您将获得有关如何绘制C2F2路易斯结构的详细逐步说明。
那么让我们继续绘制 C2F2 的路易斯结构的步骤。
绘制 C2F2 路易斯结构的步骤
步骤 1:找出 C2F2 分子中的价电子总数
为了找到 C2F2分子中的价电子总数,您首先需要知道碳原子和氟原子中存在的价电子。
(价电子是存在于任何原子最外层轨道的电子。)
在这里我将告诉您如何使用元素周期表轻松找到碳和氟的价电子。
C2F2 分子中的总价电子
→ 碳原子给出的价电子:
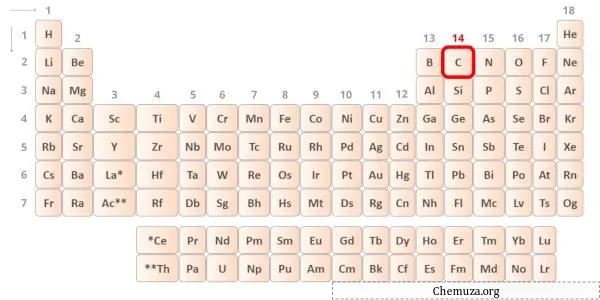
碳是元素周期表第 14 族的元素。 [1]因此,碳中存在的价电子为4 。
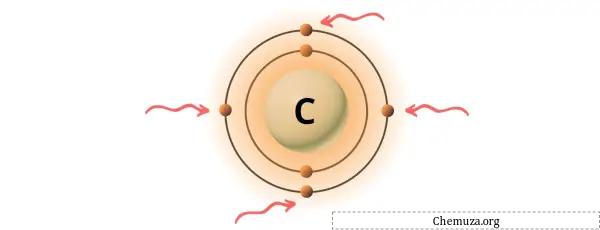
您可以看到碳原子中存在 4 个价电子,如上图所示。
→ 氟原子给出的价电子:
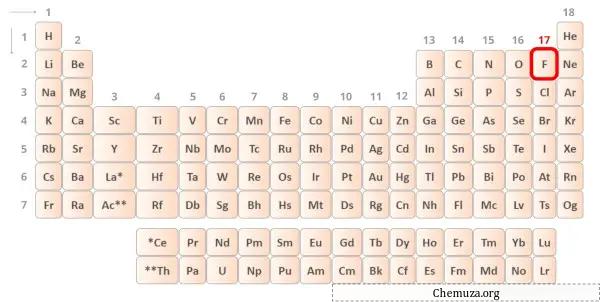
萤石是元素周期表第 17 族的元素。 [2]因此,萤石中存在的价电子为7 。
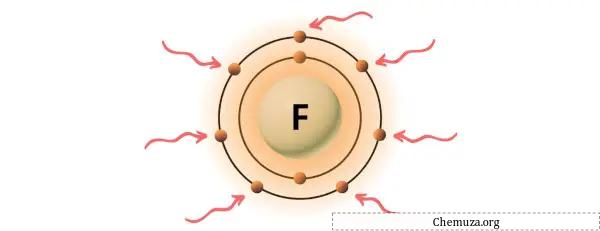
您可以看到氟原子中存在 7 个价电子,如上图所示。
所以,
C2F2分子中的总价电子= 2个碳原子贡献的价电子 + 2个氟原子贡献的价电子 = 4(2) + 7(2) = 22 。
第二步:选择中心原子
为了选择中心原子,我们必须记住电负性最小的原子保留在中心。
现在这里给定的分子是 C2F2,它包含碳 (C) 原子和氟 (F) 原子。
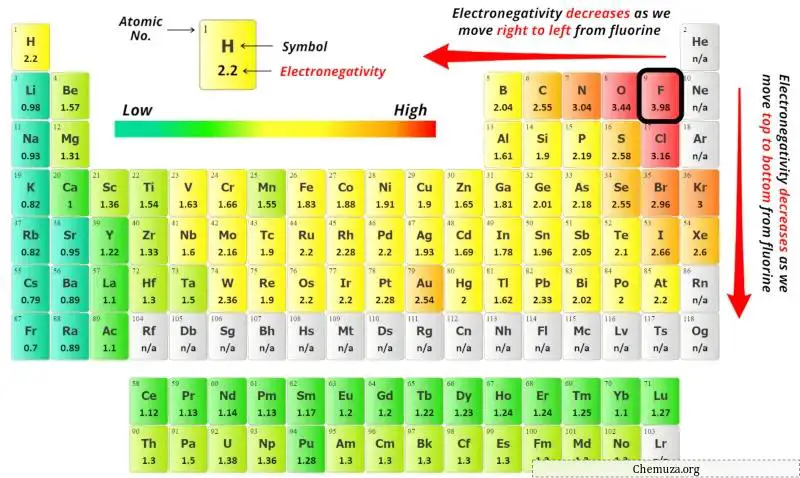
您可以在上面的元素周期表中看到碳原子(C)和氟原子(F)的电负性值。
如果我们比较碳(C)和氟(F)的电负性值,那么碳原子的电负性较小。
这里,碳(C)原子是中心原子,氟(F)原子是外部原子。
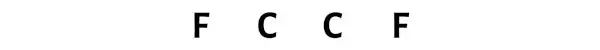
第三步:通过在原子之间放置一对电子来连接每个原子
现在,在 C2F2 分子中,您需要将电子对放置在碳-碳原子之间和碳-氟原子之间。
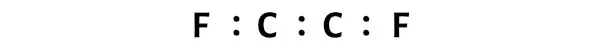
这表明这些原子在 C2F2 分子中彼此化学键合。
第四步:使外部原子稳定。将剩余的价电子对放在中心原子上。
在此步骤中,您需要检查外部原子的稳定性。
在 C2F2 分子的草图中,您可以看到外部原子是氟原子。
这些外部氟原子形成八位组,因此是稳定的。
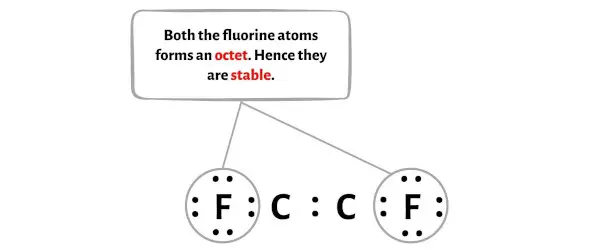
此外,在步骤 1 中,我们计算了 C2F2 分子中存在的价电子总数。
C2F2 分子共有22 个价电子,上图中仅使用了其中18 个价电子。
因此剩余电子数 = 22 – 18 = 4 。
您需要将这4 个电子放置在上图中 C2F2 分子的两个中心碳原子上。
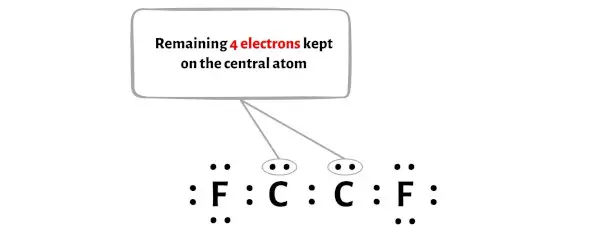
现在让我们继续下一步。
步骤5:检查中心原子上的八位字节。如果没有字节,则将孤对键转换为双键或三键。
在此步骤中,您需要检查中心碳原子(C)是否稳定。
为了检查中心碳(C)原子的稳定性,我们需要检查它们是否形成八位组。
不幸的是,两个碳原子在这里没有形成八位组。两个碳原子只有6个电子,不稳定。
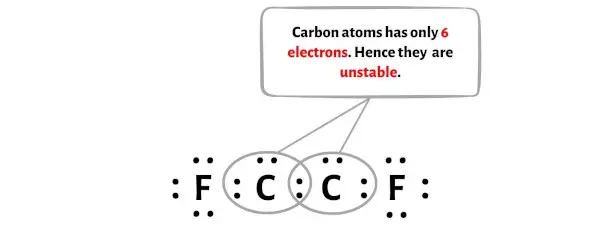
现在,为了使碳原子稳定,您需要将孤对电子对转换为双键,以便碳原子可以拥有 8 个电子(即 1 个八位组)。

但是在转换一对电子后,一个碳原子形成一个八位组,但另一个碳原子仍然没有形成八位组,因为它只有 6 个电子。
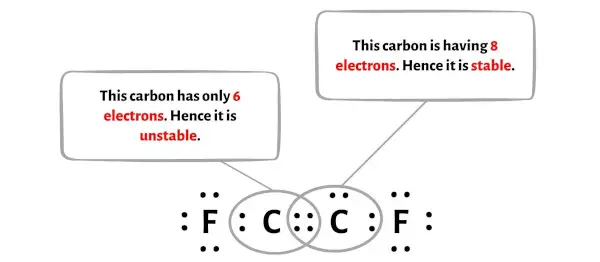
同样,我们需要转换一对额外的电子以形成三键。

当这对电子转变为三键后,中心碳原子将多获得2个电子,其总电子数将变为8。
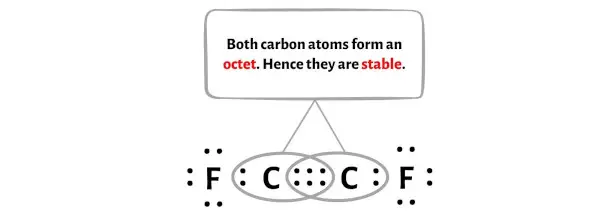
您可以在上图中看到两个碳原子形成一个八位组。
所以这些碳原子是稳定的。
现在让我们进行最后一步,检查 C2F2 的路易斯结构是否稳定。
第6步:检查路易斯结构的稳定性
现在您已完成最后一步,您需要检查 C2F2 的路易斯结构的稳定性。
路易斯结构的稳定性可以使用形式电荷概念来验证。
简而言之,我们现在必须找到 C2F2 分子中碳原子 (C) 和氟原子 (F) 上的形式电荷。
要计算正式税,您必须使用以下公式:
形式电荷 = 价电子 – (键合电子)/2 – 非键合电子
您可以在下图中看到 C2F2 分子每个原子的键合电子和非键合电子数量。
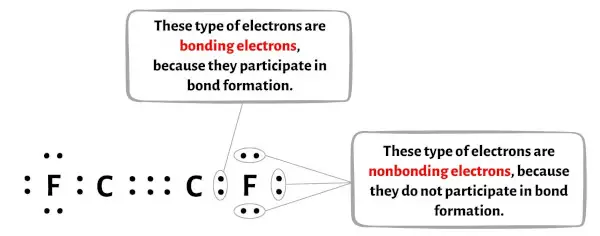
对于碳原子 (C):
价电子 = 4(因为碳属于第 14 族)
键合电子 = 8
非键合电子 = 0
对于氟原子(F):
价电子 = 7(因为萤石属于第 17 族)
键合电子 = 2
非键合电子 = 6
| 正式指控 | = | 价电子 | – | (结合电子)/2 | – | 非键合电子 | ||
| VS | = | 4 | – | 8/2 | – | 0 | = | 0 |
| F | = | 7 | – | 2/2 | – | 6 | = | 0 |
从上面的形式电荷计算中,您可以看到碳 (C) 原子和氟 (F) 原子具有“零”形式电荷。
这表明C2F2的上述Lewis结构是稳定的,C2F2的上述结构没有发生进一步的变化。
在上述C2F2的路易斯点结构中,您还可以将每对成键电子(:)表示为单键(|)。这样做将产生以下 C2F2 的路易斯结构。
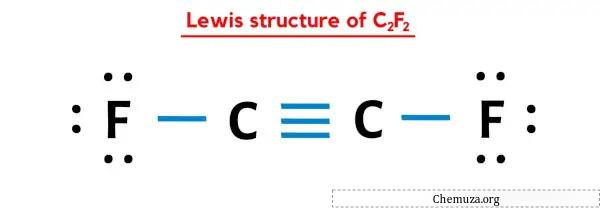
我希望您已经完全理解上述所有步骤。
为了进行更多练习和更好地理解,您可以尝试下面列出的其他路易斯结构。
尝试(或至少查看)这些路易斯结构以更好地理解:
